この記事はVivaldi Social(JP) 部活動/ビバ丼 Advent Calendar 2024 21日目の記事です.
目次
はじめに
皆さんこんにちは.初めましての方は初めまして.
現在卒論に苦しめられている,一般ビバ丼民のかすまるです.
皆さんはコミックマーケット,略してコミケというイベントをご存知でしょうか.
コミケとは,毎年お盆の時期と年末に東京ビックサイトで開催されている.日本最大の同人グッズ販売イベントです.ここには全国から同人サークルが集まり,イラスト集などの同人誌を中心に多くの同人グッズを販売しています.同人グッズが大規模に販売される機会は少ないため,コミケには膨大な数のサークルが出店し,膨大な人数のオタクがグッズを目当てに集まります.それに加えて,会場である東京ビックサイトもとても広いです.そのため,サークルを巡回する順路を工夫しなければ,グッズの購入に時間がかかってしまい,最悪の場合売り切れてしまう可能性があります.
そこで,今回は僕が現在研究している数理最適化の知識を用いて,コミックマーケットに出店しているサークルを回る順路を最適化する仕組みを考えて,実際に最適な順路を特定できるツールを開発してみたいと思います.
最適化の仕組み
※この章には高校以上で習う数学に関する記述が含まれています.必要な前提知識はなるべく少なくなるように努めますが,理解が難しい内容となっていることをご了承ください.仕組みに興味のない方は次の章まで飛ばしても構いません.
最適な経路を特定する手法について解説する前に,そもそも数理最適化とは何かについて簡単に説明します.数理最適化とは,現実の問題を数式に見立てて,いくつかの条件を満たす最も良い値の組み合わせを選択することを指します.文章だけで説明するのは難しいので,実際の数理最適化の問題を例に挙げて説明します.
例えば,次のような問題があったとします.
問題:ある工場では金属,プラスチック,ゴムという3つの原材料を用いて,2種類の電気ポッドA,Bを製造している.電気ポッドA,Bを1kg生産することで得られる利益はそれぞれ20万円,60万円である.一方,電気ポッドA,Bを1kg生産するために必要な原材料の使用量は以下の表1の通りである.また,原材料の在庫はそれぞれ金属が80kg,プラスチックが40kg,ゴムが64kgである.この時,利益が最大となる電気ポッドA,Bの生産量を求めよ.(参考文献:最適化手法入門)
| 電気ポッドA | 電気ポッドB | |
| 金属 | 5 | 4 |
| プラスチック | 2 | 4 |
| ゴム | 2 | 8 |
この問題を解くために,問題文に示された条件と最適化する対象を数式に直して行きます.電気ポッドAの生産量をx1 kg,Bの生産量をx2 kgとすると,工場の利益は以下の式で表すことができます.
20 × x1 + 60 × x2 (式1)今回は利益を最大にしたいため,式1の値が最大になるようなx1,x2の値を求めていきます.このような最適化したい式を目的関数と呼びます.また,電気ポッドA,Bを生産するために必要な原材料より,x1とx2が満たすべき条件は以下のようになります.
5 × x1 + 4 × x2 ≦ 80 (式2)2 × x1 + 4 × x2 ≦ 40 (式3)
2 × x1 + 8 × x2 ≦ 64 (式4)
x1 ≧ 0, x2 ≧ 0 (式5)
式5は,x1とx2がマイナスの値を取らないように設定しています.(x1とx2は生産量なのでマイナスにはならない)このような最適化したい値が満たすべき条件を制約条件と呼びます.
上記のような問題は線形計画問題と呼ばれ,比較的単純な手法で解くことができます.この問題を解く手法について説明すると記事がかなり長くなってしまうので省略します.興味がある方はこちらの記事などをお読みください.ちなみに,上の問題の答えはx1 = 8[kg],x2 = 6[kg]となります.
話がかなり脱線してしまいましたが,コミケの経路に関する話に戻ります.コミケを回る最適な経路を求める問題は,次のような目的を達成するための問題と言い換えることができます.
目的:行きたいサークルを全て回る経路の移動距離を最小にする
この目的を達成するために,次に示すような手順で最適な経路を求めていきます.
- コミケの会場をマス目によって構成された迷路に見立てる.
- 行きたいサークル同士を結ぶ最短移動距離を迷路探索によって求める.
- 2で求めたそれぞれのサークルを結ぶ最短移動距離を用いて,移動距離の合計が最小になるような順路を求める.
手順1では,コミケの会場をマス目によって構成された迷路に見立てます.まず,コミケでは出店しているサークルにA1などのスペース番号が割り当てられて,会場にて出店する位置が定められます.図1は,2024年夏に開催されたコミックマーケット104の地図の一部を抜粋したものです(引用元).それぞれの数字が書かれている箇所でサークルがグッズの販売を行っています.(僕もコミケに関する知識はあまりないので,間違っている箇所があれば教えてください)
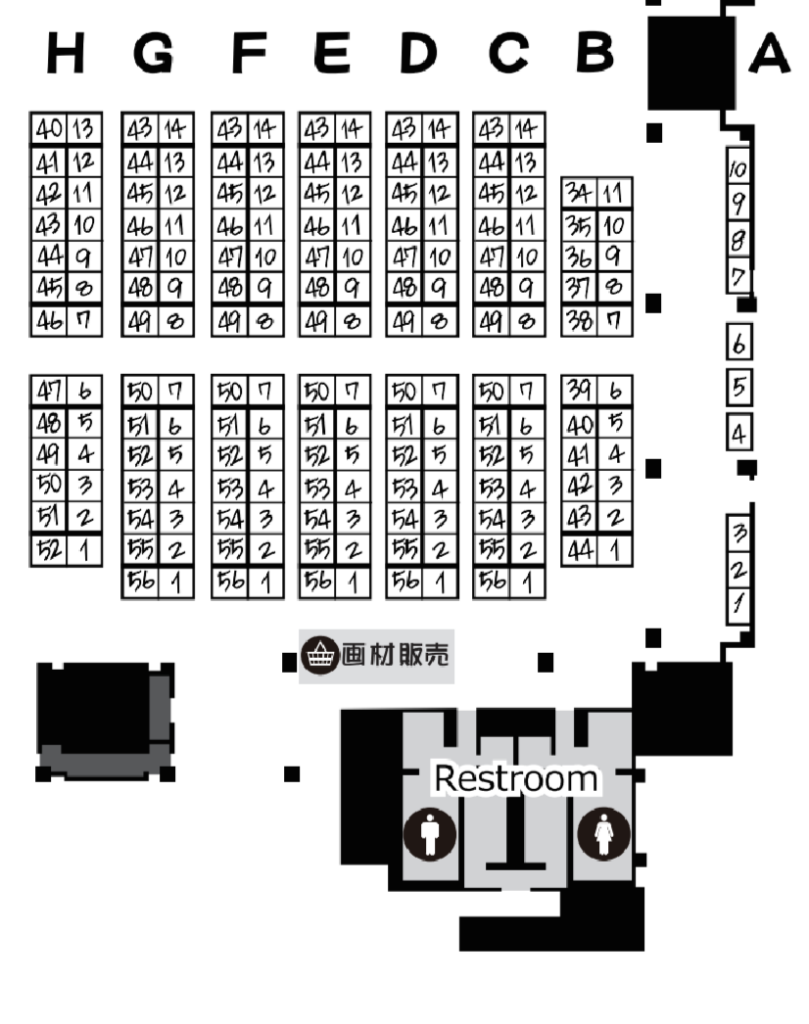
今回は,図1の範囲を経路最適化の対象とします.この地図をそのまま使用することはできないので,図2のようなマス目で構成された迷路を作成します.ここで,マス目中の0は通路,A1などは割り当てられたサークルのスペース番号,xは壁,sは会場の入口を表しています.
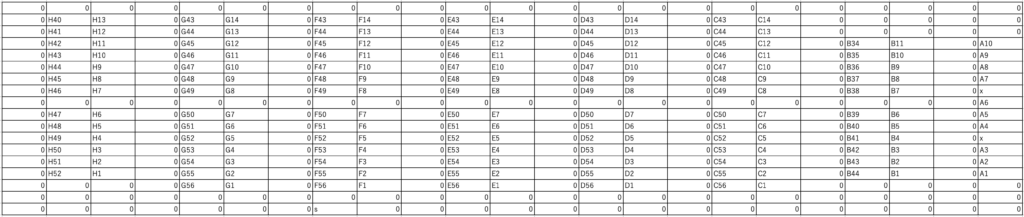
手順2では,図2のような迷路を対象に,いきたいサークル同士を結ぶ最短経路を求めていきます.まず,行きたいサークル2つを選んで,どちらか片方をスタート地点,もう一方をゴール地点とします.次に,選んだサークル以外のサークルのスペースを全て壁として,幅優先探索という手法でスタート地点からゴール地点までの最短移動距離を求めます.幅優先探索についてはこちらの記事に詳しく書かれていますので,興味のある方は読んでみてください.このような2つのサークル間の最短移動距離を行きたいサークル全ての組み合わせについて求めます.
手順3では,手順2で求めたサークル間の最短移動距離を用いて,全ての行きたいサークルを回った時の移動距離が最小となるような順路を求めます.このような移動距離が最小となるように複数箇所を訪れる順路を決定する問題は巡回セールスマン問題と呼ばれ,現在まで様々な解き方が開発されています.今回はMTZ制約を用いて,最適な順路を求めていきます.この問題の制約条件を文にすると以下のようになります.
- 全ての行きたいサークルについて,必ず1つのサークルから別の1つのサークルに向かう.
- 全ての行きたいサークルについて,別のサークルのうちどれか1つから必ずそのサークルに向かう.
- 全ての行きたいサークルを通らないような順路は作成しない.
詳しい制約条件の解説や解き方はこちらの記事が参考になりますので,そちらも合わせてご覧ください.
開発したツール
上記のような仕組みを用いて,行きたいサークル全てを回る最適な順路を求めるツールを開発しました.開発したツールは以下の「コミケ巡回経路最適化ツール」です.
リンクを開くと,図3のような複数のコードが書かれているブロックがある画面に飛ばされると思います.この画面では三角が書かれた黒丸のボタンを押すと,右に書かれているコードを実行できます.このボタンを上から順番に押して,コードを実行してください.最初のコードを実行する時に警告が表示されますが,「このまま実行」を押してください.
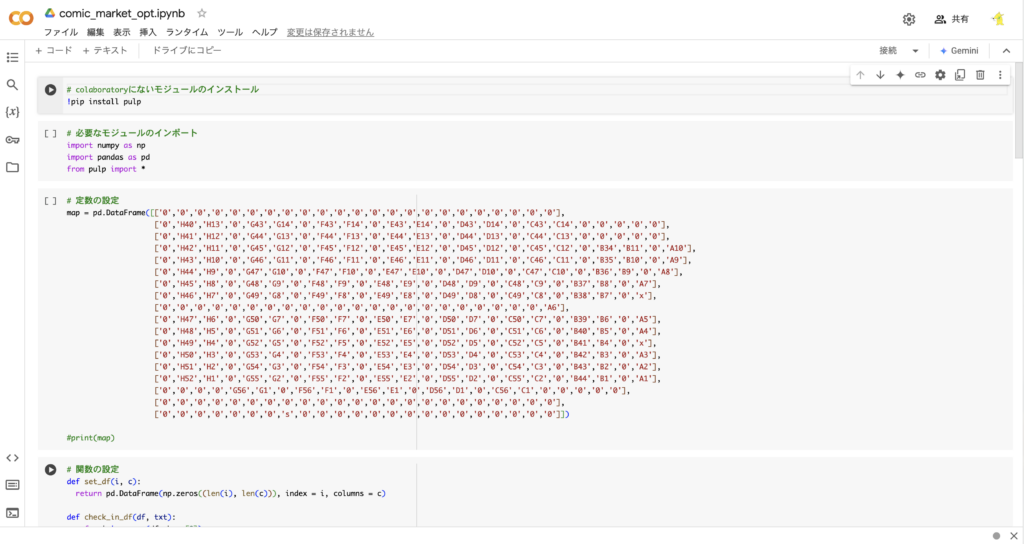
コードブロックの左に図4のようなチェックマークが付くと,そのコードが正しく実行できたことになります.コードブロックの左にチェックマークが付いてから,その下にあるコードを実行するようにしてください.
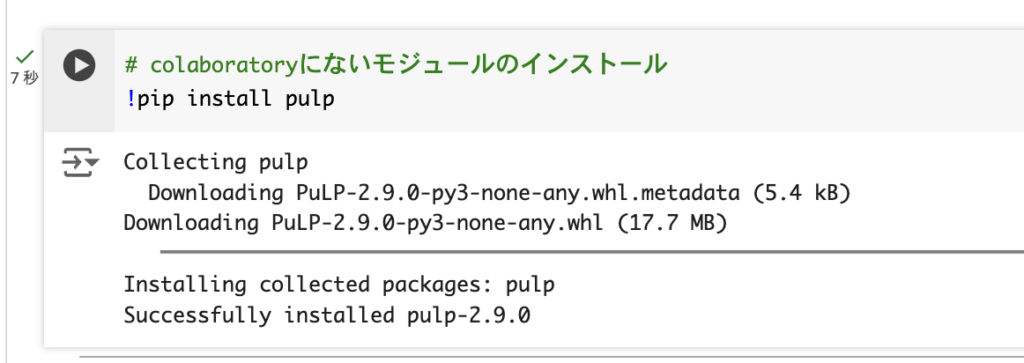
一番下のコードを実行すると,図5のような文が表示されます.「入力」の右に次の番号を入力すると,次のような操作をすることができます.
- 1:この記事の図2を参考に行きたいサークルのスペース番号を入力して,行きたいサークルリストにサークルを追加する
- 2:会場の入口から行きたいサークルリストに含まれるサークル全てを回って,入口まで戻る際の最適な順路を出力する
- 3:行きたいサークルリストをリセットする
- 0:ツールを強制的に終了する

1を入力すると,図6のように行きたいサークルのスペース番号を入力するように求められるので,図2の地図などを参考にして,スペース番号を入力してください.入力した後は,行きたいサークルリストが正しく更新されているかどうか確認してください.

2を入力すると,その時点で行きたいサークルリストに含まれているサークルについて,会場の入口からそれらのサークル全てを回って,入口に戻る順路が図7のように「通るべき順路」の下に出力されます.sは入口を表しているため,sから行きたいサークルのスペース番号を辿ることで,入口からサークルを回って戻るまでの最適な順路を知ることができます.図7の例では,最適な順路は「s→H9→A5→s」となります.

まとめ
今回はコミックマーケットのサークルを回る順路を数理最適化を用いて最適化してみました.数学の前提知識があまりない方でも理解できるような文章を書くように努めましたが,まだ分かりにくい点が多くあるかもしれません.わからないことがあれば僕のアカウントにDM等していただければ対応します.ただし,現在僕も卒論のためかなり忙しい時期に入っているため,必ず対応できるとは限らないことをご了承ください.
今回の記事によって,皆様の知見を少しでも広げられたら幸いです.
最後までご覧くださりありがとうございました.